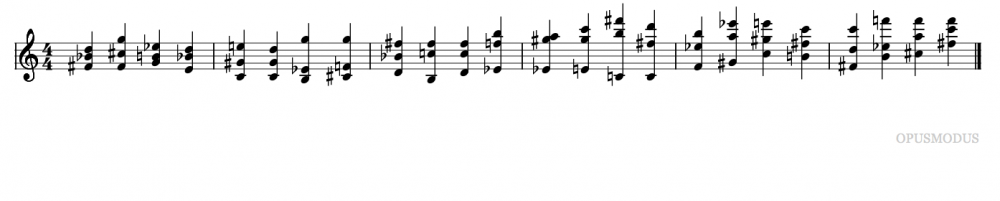Search the Community
Showing results for tags 'chords'.
-
There appears to be an issue in omitting dyads (chords) in the notation viewer when attaching attribute 'ped, as in this example: '((q c4 e3e4 ped) (q g3 c3c4 ped h e4 ped) (q c4 ped g4 e4e5 ped)) Similar issues occur when using the attribute-series function: (setf mat '((q c4 e3e4) (q g3 c3c4 h e4) (q c4 g4 e4e5))) (attribute-series '((- 1) (ped 2) (ped 4) (ped 1)) mat)
-
Is there built-in functionality to sort a chord-progression using the top note? The following example uses the bottom note: (sort-asc '(a2a3 a2a4 a2e4))
-
When I did this post, I used the Giant Steps (Coltrane) progression as harmonic path, in this way: (setf harmpath '((h (b3 maj7) (d3 7)) (h (g3 maj7) (bb3 7)) (h (eb3 maj7) (eb3 maj7)) (h (a3 m7) (d3 7)) (h (g3 maj7) (bb3 7)) (h (eb3 maj7) (gb3 7)) (h (b3 maj7) (b3 maj7)) (h (f3 m7) (bb3 7)) (h (eb3 maj7) (eb3 maj7)) (h (a3 m7) (d3 7)) (h (g3 maj7) (g3 maj7)) (h (cs3 m7) (fs3 7)) (h (b3 maj7) (b3 maj7)) (h (f3 m7) (bb3 7)) (h (eb maj7) (eb maj7)) (h (cs3 m7) (fs3 7))) But in the resulting score, the chord symbols won't show. I have some questions: 1) How to make the chord symbols appear ? 2) How to make my own custom chord symbols ? 3) Can I make associations of chord symbols with specific sets of notes ? 4) Can I display chord symbols over a melody with a Hidden Piano Part playing them ? All the best ! Julio
-
Please excuse the slightly misleading terminology in the title of this post, but I am looking for a straightforward method to experiment with different chord rhythms and patterns for the left hand in a keyboard style arrangement. As an example, I have this simple arrangement: (setf lh-chords '( #|1|# (c2 c3e3g3 c3e3g3 c3e3g3) #|2|# (f2 c3f3a3 c3f3a3 c3f3a3) #|3|# (e2 e3g3c4 e3g3c4 e3g3c4) #|4|# (gs2 e3b3 e3b3 e3b3 g2 d3g3b3 d3g3b3 d3g3b3) )) (setf lh-lengths '( #|1|# (e e e e e e e e) ;i #|2|# (e e e e e e e e) ;i #|3|# (e e e e e e e e) ;i #|4|# (e e e e e e e e) ;i )) (def-score Simple-Period (:title "Simple-Period" :key-signature '((c maj)) :rewrite-lengths 't :time-signature '((4 4 8)) :tempo '(60) ) (lh :length lh-lengths :pitch lh-chords :port "FROM Sibelius I" :channel 1 :volume 100 :pan 64 :controllers (91 '((48)) 64 '((0)))) ) Which results into: I'm pretty sure there are much easier ways to write something like this, are there any functions I can look into that make it easier to experiment with different chord inversions, arpeggio's, etc. ? It would be great if I could just write the chords first and then later in the score experiment with them, including the ability to subtract notes and alternate between bass notes and other chord tones. I've learned about gen-repeat already, which seems like it could be useful for this specific example, are any other functions I should check out? Thank you once again! - Jor
-
Here is an example of generation of harmonic progression with Opusmodus using chords rules defined with a transition table. The technique presented here uses the concept of tonal degrees, but it is important to note that as you will see later in this article, this concept can be pushed quite far and quite outside the traditional tonal system. First, we define some transition rules from degree to degree: (setf transition '((1 (4 1) (5 1) (6 2)) (2 (5 2) (4 1)) (3 (4 1)) (4 (5 1) (2 1)) (5 (1 3) (6 2) (4 1)) (6 (4 1)) (7 (1 1) (6 1)))) So here is a transition rule saying a 1st degree will be 2 times more likely to be followed by a sixth degree (1 (6 2)) as a 4th or 5th (1 (4 1) (5 1) ). A second degree will be most likely followed by a 5th degree (2 (5 2) than a 4th (2 (4 1)) We define this way all the transition rules for each degree of the scale. We now generate a sequence of degrees we call prog based on these rules with the function GEN-MARKOV-FROM-TRANSITIONS (for more information on Markov chains, you can consult: https://en.wikipedia.org/wiki/Markov_chain ): (setf prog (gen-markov-from-transitions transition :size 24 :start 1)) which can for example give this result: => (1 5 1 4 2 4 2 4 2 5 6 4 5 1 5 6 4 5 1 5 6 4 2 5) Because the function that we'll use to generate chords is based on a numbering starting from zero but our degrees generation is based on a numbering starting from 1, we will subtract 1 to each value of our list prog to able to provide our next function a number list starting from zero. To do this, we use the MAPCAR Lisp function to apply -1 to each value of the list and we store the result in the variable prog.prep. (setf prog.prep (mapcar (lambda(x) (- x 1)) prog)) => (0 4 0 3 1 3 1 3 1 4 5 3 4 0 4 5 3 4 0 4 5 3 1 4) Now we generate chords using the HARMONIC-PROGRESSION function and store the result in the variable named chords: (setf chords (harmonic-progression prog.prep '(d4 major))) The parameters passed to the function are our degrees List prog.prep and a scale with a root base (here d4). Here is the output of this function in notation: Of course, we are not limited to Major and Minor scales, we can use any scale or pitch structure available or generated by Opusmodus, here are some examples: (setf chords (harmonic-progression prog.prep '(d4 messiaen-mode5))) (setf chords (harmonic-progression prog.prep '(c4 acoustic-scale) :root '(d4 f4 g4 e4 bb3))) (setf chords (harmonic-progression prog.prep '(d4e4fs4gs4as4c5ds5) :root '(d4 f4 g4 e4 bb3))) A final example using the keyword :relative enabling a smoother transition between chords with a relative voice leading between chords. (setf chords (harmonic-progression prog.prep '(d4e4fs4gs4as4c5ds5) :root '(d4 f4 g4 e4 bb3) :relative t)) Once these chords generated, you can use them as you want in Opusmodus, map them on musical structures with TONALITY-MAP function or use them as basic materials to create reservoirs of pitch or other kind of pitch material. SB.
- 5 replies
-
- chords
- progression
-
(and 1 more)
Tagged with:
-
Bonjour, Lors d'une recherche dans la librairie d'Opusmodus, il me semble que j'avais trouvé toute la liste des accords en notation "jazz" en Do pouvant-être associée au mot clé :rotate pour les renversements. Mais je ne la retrouve plus. Aurais-je confondu avec le document "Accords noms" qui propose une liste plus limitée d'accords ? Merci d'avance. Didier Hello, During a search in the library of Opusmodus, I think I found the whole list of rating chords "jazz" in C that can be associated with the keyword :rotate to inversion/rotation. But I found the most. Would I confused with the document "Accords noms" which offers a more limited list of chords? Thank you in advance. PS : Sorry for my bad english.