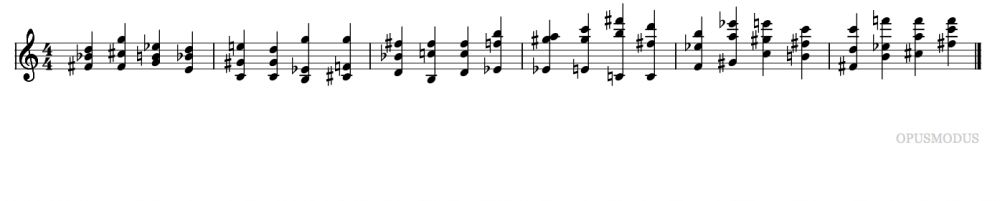Search the Community

Here is an example of generation of harmonic progression with Opusmodus using chords rules defined with a transition table. The technique presented here uses the concept of tonal degrees, but it is important to note that as you will see later in this article, this concept can be pushed quite far and quite outside the traditional tonal system. First, we define some transition rules from degree to degree: (setf transition '((1 (4 1) (5 1) (6 2)) (2 (5 2) (4 1)) (3 (4 1)) (4 (5 1) (2 1)) (5 (1 3) (6 2) (4 1)) (6 (4 1)) (7 (1 1) (6 1)))) So here is a transition rule saying a 1st degree will be 2 times more likely to be followed by a sixth degree (1 (6 2)) as a 4th or 5th (1 (4 1) (5 1) ). A second degree will be most likely followed by a 5th degree (2 (5 2) than a 4th (2 (4 1)) We define this way all the transition rules for each degree of the scale. We now generate a sequence of degrees we call prog based on these rules with the function GEN-MARKOV-FROM-TRANSITIONS (for more information on Markov chains, you can consult: https://en.wikipedia.org/wiki/Markov_chain ): (setf prog (gen-markov-from-transitions transition :size 24 :start 1)) which can for example give this result: => (1 5 1 4 2 4 2 4 2 5 6 4 5 1 5 6 4 5 1 5 6 4 2 5) Because the function that we'll use to generate chords is based on a numbering starting from zero but our degrees generation is based on a numbering starting from 1, we will subtract 1 to each value of our list prog to able to provide our next function a number list starting from zero. To do this, we use the MAPCAR Lisp function to apply -1 to each value of the list and we store the result in the variable prog.prep. (setf prog.prep (mapcar (lambda(x) (- x 1)) prog)) => (0 4 0 3 1 3 1 3 1 4 5 3 4 0 4 5 3 4 0 4 5 3 1 4) Now we generate chords using the HARMONIC-PROGRESSION function and store the result in the variable named chords: (setf chords (harmonic-progression prog.prep '(d4 major))) The parameters passed to the function are our degrees List prog.prep and a scale with a root base (here d4). Here is the output of this function in notation: Of course, we are not limited to Major and Minor scales, we can use any scale or pitch structure available or generated by Opusmodus, here are some examples: (setf chords (harmonic-progression prog.prep '(d4 messiaen-mode5))) (setf chords (harmonic-progression prog.prep '(c4 acoustic-scale) :root '(d4 f4 g4 e4 bb3))) (setf chords (harmonic-progression prog.prep '(d4e4fs4gs4as4c5ds5) :root '(d4 f4 g4 e4 bb3))) A final example using the keyword :relative enabling a smoother transition between chords with a relative voice leading between chords. (setf chords (harmonic-progression prog.prep '(d4e4fs4gs4as4c5ds5) :root '(d4 f4 g4 e4 bb3) :relative t)) Once these chords generated, you can use them as you want in Opusmodus, map them on musical structures with TONALITY-MAP function or use them as basic materials to create reservoirs of pitch or other kind of pitch material. SB.

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;gen-chained-sym-vals.by-markov;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;; special-symm-sequences ;;; have look at the possible parameters (&key) ;;; it's generates symm-structures via MARKOV ;;; and the could be "chained" between generations ;;; also with symm.structures... like: (also look at CARTER's work) ;;; => ((1 2 5 8 5 2 1) (3 1 2 2 2 1 3) (8 1 3 1 8) (3 1 2 2 2 1 3) (1 2 5 8 5 2 1)) ;;; chains: 2 1 3 1 2 2 1 3 1 2 ;;; or: ;;; => ((e4 f4 c4 e4 d4 e4 c4 f4 e4) (c4 e4 f4 c4 fs4 c4 f4 e4 c4) (e4 fs4 f4 fs4 e4) (c4 e4 f4 c4 fs4 c4 f4 e4 c4) (e4 f4 c4 e4 d4... ;;; chains: c4 f4 e4 c4 e4 f4 c4 e4 c4 e4 e4 c4 e4 ........etc....... ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;; main function with amateur-code :-) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; (defun gen-chained-sym-vals.by-markov (&key (generations 'nil) (non-symmetric 'nil) (number-of-vals 20) (basic-seq-lengths '(3 5)) (transition-matrix '((1 (4 1) (5 1) (6 2)) (2 (5 2) (4 1)) (3 (4 1)) (4 (5 1) (2 1)) (5 (1 3) (6 2) (4 1)) (6 (4 1)) (7 (1 1) (6 1)))) (chain-weight 1.0) (possible-chain-length '(1 2 3)) (reduction 0.0) (start-value (car (car transition-matrix)))) (let ((sequence1 0) (sequence2 0) (seq-lengths basic-seq-lengths)) (setq sequence1 (loop repeat (if (equal generations 'nil) (car (list number-of-vals)) (if (equal non-symmetric 'nil) (if (evenp generations) (/ generations 2) (/ (1- generations) 2)) (car (list generations)))) with seq1 with seq with chain1 with slot = (second (gen-markov-from-transitions transition-matrix :size 2 :start start-value)) with seq-splitter = (gen-markov-from-transitions transition-matrix :size (rnd-pick possible-chain-length) :start slot) with seq-lengths = basic-seq-lengths when (equal (prob? chain-weight) 't) do (setq chain1 (append (list (setq slot (second (gen-markov-from-transitions transition-matrix :size 2 :start slot)))) seq-splitter (list (setq slot (second (gen-markov-from-transitions transition-matrix :size 2 :start slot)))))) and do (setq seq (append (butlast chain1) (reverse chain1))) and collect (if (equal (prob? reduction) 't) (append (setq seq (butlast (rest seq)))) (append seq)) else collect (setq seq1 (gen-markov-from-transitions transition-matrix :size (rnd-pick seq-lengths) :start slot) seq (append seq1 (reverse seq1))) do (setq seq-splitter (reverse (filter-last (rnd-pick possible-chain-length) seq))))) (if (equal generations 'nil) (progn (setq sequence2 (filter-first (if (evenp number-of-vals) (/ number-of-vals 2) (/ (1- number-of-vals) 2)) (flatten sequence1))) (if (evenp number-of-vals) (append sequence2 (reverse sequence2)) (append sequence2 (list (rnd-pick (flatten (filter-first 1 transition-matrix)))) (reverse sequence2)))) (if (equal non-symmetric 'nil) (if (evenp generations) (append sequence1 (reverse sequence1)) (append sequence1 (list (gen-sym-markov :seq-length (rnd-pick seq-lengths) :transition-matrix transition-matrix)) (reverse sequence1))) (append sequence1))))) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;; test it! ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; (gen-chained-sym-vals.by-markov :generations 5 :transition-matrix '((1 (2 1) (3 3) (5 2) (8 1)) (2 (1 2) (5 3)) (3 (1 2) (8 1) (2 3)) (5 (3 2) (2 1) (1 3)) (8 (1 2) (2 2) (3 1)))) (gen-chained-sym-vals.by-markov :generations 5 :transition-matrix '((c4 (d4 1) (e4 3) (f4 2) (fs4 1)) (d4 (c4 2) (f4 3)) (e4 (c4 2) (fs4 1) (d4 3)) (f4 (e4 2) (d4 1) (c4 3)) (fs4 (c4 2) (d4 2) (e4 1)))) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;; WHEN PATTERN-MATCH => T ;;; THEN MARKOV PRODUCES THE NEXT VALUES ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; subfunctions (defun pattern-match (liste pattern) (loop for z in liste with cnt = 0 with pattern_cnt = 0 when (or (equal (nth cnt pattern) z) (equal '? (nth cnt pattern))) do (incf pattern_cnt) and do (incf cnt) else do (setq cnt (setq pattern_cnt 0)) when (equal pattern_cnt (length pattern)) collect 't into bag and do (return (car bag)))) (defun test.pm.omn (seq pattern) (let ((seq (if (omn-formp seq) (cond ((lengthp (car pattern)) (omn :length seq)) ((pitchp (car pattern))(omn :pitch seq)) ((velocityp (car pattern)) (omn :velocity seq))) (append seq)))) (pattern-match seq pattern))) ;; mainfuction (defun test.pm+markov (seq pattern start-slot transitions &key (size 1)) (if (test.pm.omn seq pattern) (if (= size 1) (car (rest (gen-markov-from-transitions transitions :size (1+ size) :start start-slot))) (rest (gen-markov-from-transitions transitions :size (1+ size) :start start-slot))) (append start-slot))) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; (setf transitions '((a (a 2) (b 1)) (b (a 2) (b 1)))) (setq test-omn '(t fs4 pp tasto g4 ppp tasto -s. t e4 pppp tasto -s. t eb4 pp tasto -het - t)) ;; examples1 (test.pm+markov test-omn '(pp ppp) 'a transitions) ;; evaluate a few times (test.pm+markov test-omn '(fs4 g4) 'a transitions) ;; evaluate a few times (test.pm+markov test-omn '(g2) 'a transitions) ;; evaluate a few times => no match => no new value (test.pm+markov test-omn '(1/32 -3/32) 'a transitions) ;; evaluate a few times ;; examples2 (test.pm+markov test-omn '(pp) 'a transitions :size 5) ;; evaluate a few times (test.pm+markov test-omn '(g4 e4) 'a transitions :size 3) ;; evaluate a few times ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

a concrete example (but musical-nonsense)... of a TRANSITION produced by a special markov-program 1) functions/subfuctions ;;;;;;;;;;;;;;;;;;;;;;;;;;;; (defun add-transition-weight (transition-list value add-weight) (loop for j in transition-list collect (append (list (first j)) (loop repeat (1- (length j)) for cnt = 1 then (incf cnt) when (equal (first (nth cnt j)) value) collect (list (first (nth cnt j)) (+ add-weight (second (nth cnt j)))) else collect (nth cnt j))))) ;;;;;;;;;;;;;;;;;;;;;;;;;; (defun count-repetitions (value-list) (let ((seq (append value-list (list 'nil)))) (loop repeat (1- (length seq)) with count = 1 for cnt1 = 0 then (incf cnt1) for cnt2 = 1 then (incf cnt2) when (equal (nth cnt1 seq) (nth cnt2 seq)) do (incf count) when (not (equal (nth cnt1 seq) (nth cnt2 seq))) collect count and do (setq count 1)))) ;;;;;;;;;;;;;;;;;;;;;;;;;;; (defun eliminate-repetitions (liste) (let ((liste (append liste (list 'nil)))) (loop repeat (1- (length liste)) with cnt = 0 when (not (equal (nth cnt liste) (nth (+ 1 cnt) liste))) collect (nth cnt liste) do (incf cnt)))) (eliminate-repetitions '(1 1 2 3 4 4 4 1 1 2)) ;;;;;;;;;;;;;;;;;;;;;;;;;;;; (defun gen-markov-from-transitions-with-tendency (transitions size generations value &key (add-weight 1) (start (first (first transitions)))) (loop repeat generations with list = (gen-markov-from-transitions transitions :size size :start start ) with weight = add-weight with weight-growth = 0 do (setq transitions (add-transition-weight transitions value weight)) append (setq list (gen-markov-from-transitions transitions :size size :start (filter-first-last 1 list))) do (incf weight (incf weight-growth)))) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; 2) example and possible implementation => create a TRANSITION to value 3 (=> to pitch eb4) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;;;evaluate a few times, to check it;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; (list-plot ;;non-neutral-table (setq integers (gen-markov-from-transitions-with-tendency '((1 (1 1) (2 4) (3 1)) (2 (1 1) (4 1) (3 3)) (3 (1 4) (3 5) (4 3)) (4 (1 1) (3 2) (4 3))) 10 20 3 :add-weight 3)) :point-radius 0 :style :fill) #| ;;another example with different mapping (list-plot ;;non-neutral-table (setq integers (gen-markov-from-transitions-with-tendency '((1 (1 1) (2 4) (3 1)) (2 (1 1) (4 1) (3 3) (6 1)) (3 (1 4) (3 5) (4 3) (6 1) (5 1)) (4 (1 1) (3 2) (4 3) (5 2) (6 1)) (5 (1 1) (3 1) (4 1)) (6 (2 3) (1 2) (3 1) (5 1))) 10 20 3 :add-weight 3)) :point-radius 0 :style :fill) (setq integers (replace-map '((5 -5) (1 0) (2 6) (3 14) (4 20) (6 25)) integers)) |# ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;;;;;gen an example-score;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; (def-score example (:key-signature 'chromatic :time-signature '(4 8) :tempo '(e 176) :layout (bracket-group (piano-grand-layout 'piano))) (piano :omn (make-omn :pitch (eliminate-repetitions (integer-to-pitch integers)) :length (gen-length (count-repetitions integers) 1/32)) :sound 'gm-piano))

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;another little markov-game => markov with "global-tendency" ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;;a "neutral table with 4 values" (setq transitions '((1 (1 1) (2 1) (3 1) (4 1)) (2 (1 1) (2 1) (3 1) (4 1)) (3 (1 1) (2 1) (3 1) (4 1)) (3 (1 1) (2 1) (3 1) (4 1)) (4 (1 1) (2 1) (3 1) (4 1)))) ;;;subfunctions (defun filter-first-last (n sequence) (car (filter-last n sequence))) (defun substitute-transition-weight (transition-list value new-weight) (loop for j in transition-list collect (append (list (first j)) (loop repeat (1- (length j)) for cnt = 1 then (incf cnt) when (equal (first (nth cnt j)) value) collect (list (first (nth cnt j)) new-weight) else collect (nth cnt j))))) ;;;mainfuction (defun markov-with-tendency (transitions size generations value) (loop repeat generations with list = (gen-markov-from-transitions transitions :size size :start 1) with weight = 1 with weight-add = 0 do (setq transitions (substitute-transition-weight transitions value weight)) append (setq list (gen-markov-from-transitions transitions :size size :start (filter-first-last 1 list))) do (incf weight (incf weight-add)))) ;;;some simulations => evaluate!!! (list-plot (markov-with-tendency transitions 10 20 1) :point-radius 0 :style :fill) (list-plot (list (markov-with-tendency transitions 10 20 1) (markov-with-tendency transitions 10 20 2) (markov-with-tendency transitions 10 20 4)) :point-radius 0 :style :fill) (list-plot ;;non-neutral-table (markov-with-tendency '((1 (1 1) (2 4)) (2 (1 1) (4 1)) (3 (1 4) (3 5) (4 3)) (3 (1 1) (2 4) (3 2)) (4 (1 1) (3 2) (4 3))) 10 20 1) :point-radius 0 :style :fill)

;;;little markov-game: ;;;gen-markov => analyze the output => produce new rules => gen-markov ;;;make x-times the list-plot and you will see how the system most of the times ;;;comes to a "constant STATE" (defun self-analyzing/generating-markov (transitions size generations) (loop repeat generations with list = (gen-markov-from-transitions transitions :size size :start 1) append (setq list (gen-markov-from-transitions (gen-markov-transitions list) :size size :start (car (last list)))))) ;;;a "neutral table with 4 values" (setf transition-table '((1 (1 1) (2 1) (3 1) (4 1)) (2 (1 1) (2 1) (3 1) (4 1)) (3 (1 1) (2 1) (3 1) (4 1)) (3 (1 1) (2 1) (3 1) (4 1)) (4 (1 1) (2 1) (3 1) (4 1)))) ;;;evaluate a few times and have a look on the output (list-plot (self-analyzing/generating-markov transition-table 20 20) :point-radius 0 :style :fill)

i'm working on a program including "markov"... so i coded this small FUNCTION to SUBSTITUTE markov-rules-values (because in my "project" i'm generating a feedback on the markov-rules (after a pattern-match)). i know it could be coded a lot smarter but it works. have fun! andré ;;;;FUNCTION (defun substitute-transition-value (transition-list value-old value-new) (loop for j in transition-list collect (loop for i in j when (numberp i) append (substitute value-new value-old (list i)) when (listp i) collect (append (substitute value-new value-old (list (first i))) (list (second i)))))) ;;;;;EXAMPLE (setq transitions '((1 (2 1) (3 3) (5 2) (8 1)) (2 (1 2) (5 3)) (3 (1 2) (8 1) (2 3)) (5 (3 2) (2 1) (1 3)) (8 (1 2) (2 2) (3 1)))) (substitute-transition-value transitions 1 -1) => ((-1 (2 1) (3 3) (5 2) (8 1)) (2 (-1 2) (5 3)) (3 (-1 2) (8 1) (2 3)) (5 (3 2) (2 1) (-1 3)) (8 (-1 2) (2 2) (3 1)))

hi all, i'm looking for a markov-function who's working with a transition-table (like in OPMO), but who is "context-sensitive". the table could be something like that (but nonsense-example here): (setq transition-table '((1 (2 1) (3 1)) (2 ((1 3) 1) (2 1)) (3 (1 1) (4 1)) (1 3 (2 1) ((3 1) 1)))) is there any "hidden-function" in OPUSMODUS, or have i code it for myself? ...it makes "musically" more sense to work with context- then with single-value-decisions... thanx andré

hi all, i coded a little markov-program who changes the LEVEL-size if necessary to generate the number of values you want exactly. it would be nice if someone could check/test the IDEA, and if it's correct and makes sense :-) the markov starts on LEVEL 3 and tries to generate a number of output-levels with its TRANSITION-rules (level-3-rules), if it's possible (=generating the size) everything's fine. but if it's not possible, then the programm changes on LEVEL-2-rules ... if this is also not possible (to generate the size) then it changes to LEVEL 1... here is the code... ;;;FUNCTION (defun gen-multiple-markov (sequence &key size) (let ((transitions-level-1 (gen-markov-transitions sequence :level 1)) ;; gen transition-table level-1 (transitions-level-2 (gen-markov-transitions sequence :level 2)) ;; gen transition-table level-2 (seq (gen-markov-from-transitions (gen-markov-transitions sequence :level 3) :size size))) ;; gen markov-seq on level-3 (if (< (length seq) size) ;; test if seq is too short (/= (length seq) size) (progn ;; if too short -> combine the last seq with a new one (level 2) (setq seq (append seq (gen-markov-from-transitions transitions-level-2 :size (- size (length seq)) :start (last seq)))) (if (< (length seq) size) ;; same test as above (append (append seq (gen-markov-from-transitions transitions-level-1 :size (- size (length seq)) :start (last seq)))) (append seq))) (append seq)))) ;;;TEST (gen-multiple-markov '(1 2 3 2 1 2 3 2 1 2 2 2 2 1 1 1 1 2 2 3 2 1 1 2) :size 36) best wishes and THANX andré

;;;;small function -> create symmetrical lists (palindrom) with markov (for generating half-seq) (setf transition '((1 (4 1) (5 1) (-6 2)) (2 (5 2) (4 1)) (3 (4 1)) (4 (5 1) (2 1)) (5 (1 3) (-6 2) (4 1)) (-6 (4 1) (3 2)) (7 (1 1) (-6 1)))) ;;;FUNCTION (defun gen-sym-markov (&key seq-length transition-matrix) (let ((vals 0)) ;falls seq-length = liste, werden positive werte gezählt und neu ;seq-length (= angepasst, formatunabhängig) (if (listp seq-length) (setq seq-length (car (last (loop for i in seq-length with cnt = 0 when (> i 0) collect (incf cnt)))))) ;entscheindung grad/ungrad (if (evenp seq-length) (progn (setq vals (gen-markov-from-transitions transition-matrix :size (/ seq-length 2) :start (rnd-pick (flatten (filter-first 1 transition-matrix))))) (append vals (reverse vals))) (progn (setq vals (gen-markov-from-transitions transition-matrix :size (/ (- seq-length 1) 2) :start (rnd-pick (flatten (filter-first 1 transition-matrix))))) (append vals (list (rnd-pick (flatten (filter-first 1 transition-matrix)))) (reverse vals)))))) ;;;;EXAMPLE (gen-sym-markov :seq-length 8 :transition-matrix transition)