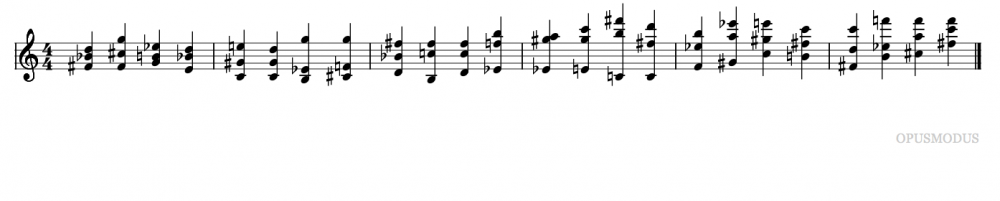Search the Community
Showing results for tags 'progression'.
-
Here is an example of generation of harmonic progression with Opusmodus using chords rules defined with a transition table. The technique presented here uses the concept of tonal degrees, but it is important to note that as you will see later in this article, this concept can be pushed quite far and quite outside the traditional tonal system. First, we define some transition rules from degree to degree: (setf transition '((1 (4 1) (5 1) (6 2)) (2 (5 2) (4 1)) (3 (4 1)) (4 (5 1) (2 1)) (5 (1 3) (6 2) (4 1)) (6 (4 1)) (7 (1 1) (6 1)))) So here is a transition rule saying a 1st degree will be 2 times more likely to be followed by a sixth degree (1 (6 2)) as a 4th or 5th (1 (4 1) (5 1) ). A second degree will be most likely followed by a 5th degree (2 (5 2) than a 4th (2 (4 1)) We define this way all the transition rules for each degree of the scale. We now generate a sequence of degrees we call prog based on these rules with the function GEN-MARKOV-FROM-TRANSITIONS (for more information on Markov chains, you can consult: https://en.wikipedia.org/wiki/Markov_chain ): (setf prog (gen-markov-from-transitions transition :size 24 :start 1)) which can for example give this result: => (1 5 1 4 2 4 2 4 2 5 6 4 5 1 5 6 4 5 1 5 6 4 2 5) Because the function that we'll use to generate chords is based on a numbering starting from zero but our degrees generation is based on a numbering starting from 1, we will subtract 1 to each value of our list prog to able to provide our next function a number list starting from zero. To do this, we use the MAPCAR Lisp function to apply -1 to each value of the list and we store the result in the variable prog.prep. (setf prog.prep (mapcar (lambda(x) (- x 1)) prog)) => (0 4 0 3 1 3 1 3 1 4 5 3 4 0 4 5 3 4 0 4 5 3 1 4) Now we generate chords using the HARMONIC-PROGRESSION function and store the result in the variable named chords: (setf chords (harmonic-progression prog.prep '(d4 major))) The parameters passed to the function are our degrees List prog.prep and a scale with a root base (here d4). Here is the output of this function in notation: Of course, we are not limited to Major and Minor scales, we can use any scale or pitch structure available or generated by Opusmodus, here are some examples: (setf chords (harmonic-progression prog.prep '(d4 messiaen-mode5))) (setf chords (harmonic-progression prog.prep '(c4 acoustic-scale) :root '(d4 f4 g4 e4 bb3))) (setf chords (harmonic-progression prog.prep '(d4e4fs4gs4as4c5ds5) :root '(d4 f4 g4 e4 bb3))) A final example using the keyword :relative enabling a smoother transition between chords with a relative voice leading between chords. (setf chords (harmonic-progression prog.prep '(d4e4fs4gs4as4c5ds5) :root '(d4 f4 g4 e4 bb3) :relative t)) Once these chords generated, you can use them as you want in Opusmodus, map them on musical structures with TONALITY-MAP function or use them as basic materials to create reservoirs of pitch or other kind of pitch material. SB.
- 5 replies
-
- chords
- progression
-
(and 1 more)
Tagged with: