JulioHerrlein

Yes, the learning curve is high, but there are a lot of benefits in this way of thinking music, specially if You work with notated music. This is where Opusmodus fill the gap, making a Bridge between code, algorhythms and notation in a desktop work flow, where you can organize all your files and stuff without distractions. Best, Julio

Wow!!!! The future version!!! This is cool! Best Julio

Thanks a lot, Stephane !! Best ! Julio

Dear All, Stephane did this amazing and clear example (code below) of how to spread an harmonic progression over a predefined texture. This can be altered to any harmonic idiom. I did some test, using a chorale texture originated from a 12-tone row and also a more jazz-oriented chorale. THE QUESTION IS (For Stephane Boussuge) 1) How the harmonic rhythm is controlled here? In the example, the chord changes every half note. 2) How can I make the harmony changes at every quarter note ? 3) Can I use different rates of harmonic rhythms ? Best, Julio ;;; Classical Accompaniment Exemple ;;;--------------------------------------------------------- ;;; Parameters ;;;--------------------------------------------------------- ;;; Motif definition (setf mtf1 '((s c5 leg g5 leg e6 leg g5 c5 leg g5 leg e6 leg g5))) (setf mtf2 (pitch-transpose 4 mtf1)) (setf mtf3 '((-q e5))) (setf mtf4 '((-q g4c5))) (setf mtf5 '((q c2 -))) ;;; Chords definition (setf chords (library 'harmoprog1 'minor-4vx 'prog1)) ;;; Ostinati (setf ost1 (gen-repeat (length chords) mtf1)) (setf ost2 (gen-repeat (length chords) mtf2)) (setf ost3 (gen-repeat (length chords) mtf3)) (setf ost4 (gen-repeat (length chords) mtf4)) (setf ost5 (gen-repeat (length chords) mtf5)) ;;; Tonality-map series (setf tm-path (tonality-series chords)) ;;; Here we apply the map 'tm-path' into arpegio sequence. (setf ost1.map (tonality-map tm-path ost1)) (setf ost2.map (tonality-map tm-path ost2)) ;;; Here we apply our library chords into chord sequence. ;;; The harmonic-path preserves the voice leading. (setf ost3.map (harmonic-path chords ost3)) (setf ost4.map (harmonic-path chords ost4)) (setf ost5.map (harmonic-path chords ost5)) (setf violin1 (ambitus '(g3 c7) ost2.map)) (setf violin2 (ambitus '(g3 c6) ost1.map)) (setf viola (ambitus '(c3 e4) ost3.map)) (setf violoncello (ambitus-chord 12 (pitch-transpose -12 ost4.map))) (setf bass ost5.map) ;;;--------------------------------------------------------- ;;; Score and Layout ;;;--------------------------------------------------------- (def-score Classical-accomp (:title "Classical accompaniment example" :composer "S.Boussuge" :copyright "Copyright © 2018 s.boussuge" :key-signature 'chromatic :time-signature '((1 1 1 1) 4) :tempo 80 :layout (bracket-group (violin-layout 'violin1 :name "Violin-1") (violin-layout 'violin2 :name "Violin-2") (viola-layout 'viola) (violoncello-layout 'violoncello) (contrabass-layout 'bass) ) ) (violin1 :omn violin1 :channel 1 :sound 'gm :program 'String-Ensemble-1 :volume 100 :pan 48 :controllers (91 '(68)) ) (violin2 :omn violin2 :channel 2 :sound 'gm :program 'String-Ensemble-1 :volume 100 :pan 48 :controllers (91 '(68)) ) (viola :omn viola :channel 3 :sound 'gm :program 'String-Ensemble-1 :volume 90 :pan 64 :controllers (91 '(68)) ) (violoncello :omn violoncello :channel 4 :sound 'gm :program 'String-Ensemble-1 :volume 90 :pan 80 :controllers (91 '(68)) ) (bass :omn bass :channel 5 :sound 'gm :program 'String-Ensemble-1 :volume 90 :pan 80 :controllers (91 '(68)) ) )

Thanks, Stephane!!! All the best! Julio

Great !! Opmo Score avaiable ? Best, Julio

Really nice!

Great work, Stephane ! Congrats ! Julio

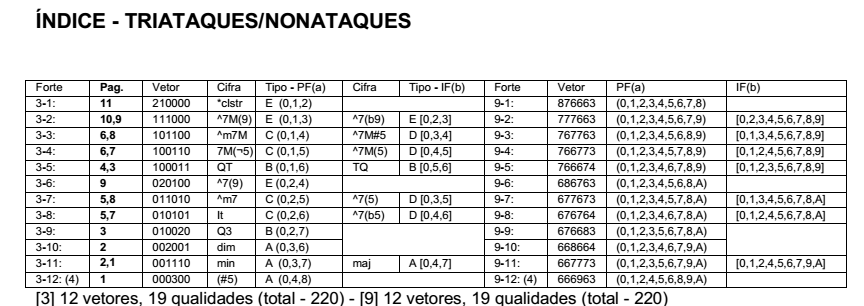
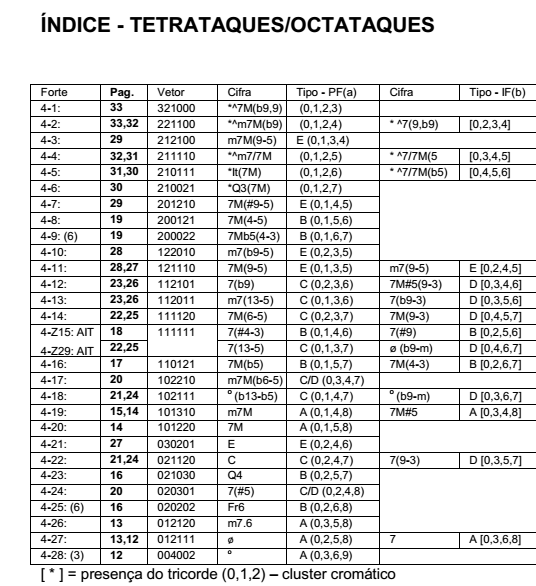
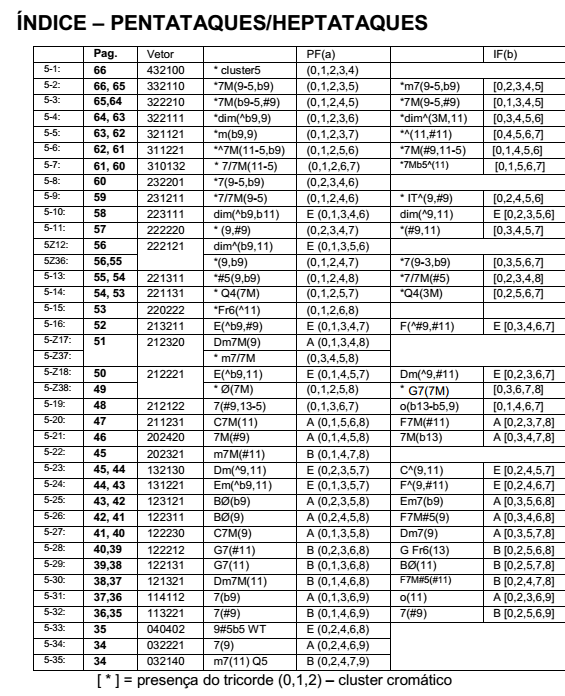
I did my own chord symbols for all the FORTE Structures (p. 361 of Dissertation ). Just in case... Some have Strange names, specially the chords that contain a Chromatic Cluster. Best, Julio

WOWWWWWWWWWWWWWWWWWWWWWWW I´m CRAZY to have IT !!!!! Thanks a lot !!!! When it is going to be released ? BEST !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! :) :) :) :) :) :) :) :) :) :) :) :)

Thanks, Stephane ! Best, Julio

The chords are also derived from the slonimsky patterns? Do you remember wich slonimsky pattern you used? Im teaching slonimsky patterns to my students and using opusmodus in the class. This is Great! Best Julio

Sounds Great, Stephane! Somewhat jazzy and groovy in my perception. Any hint of the code/method used? Best!

Thanks a lot, Janusz! Let me know if you find something wrong. Looking forward for this function. Looks Great! Best, Julio

Dear Janusz, Yes, I did a mistake in the dissertation caption of this example but in the attached complete catalog of the Dissertation it's correct. The complete rotations of the 4-24 set are like this (page 388 of the dissertation): Thank you ! Julio

Thank you, Janusz ! Looking Forward to have it ! Best ! Julio

WOW !!!!!!!!!!!!!!!!!!! Amazing !!!! This is great !!!!! MUCH LOVE !!! Thanks ! Next release ? All the best !! Julio LOOKING FORWARD !!!!!!!!!!!!!!!!!!!!!!!!!!!! THIS IS THE Coolest thing !!! hahahahahaha

Thanks a lot, Janusz !! Looking forward to next release of Opusmodus. All the best ! Julio

I'm very Happy to see your work, Janusz! Thank you for all your Hard work in Opusmodus! All the best! Julio added 7 minutes later André Meier came with something interesting in this post: Best, Julio

Thanks a lot! Great article and ideas. Best, Julio

Marvellous, Stephane !! Thanks ! Julio

After we figure out the pattern sequence, gen-sive or make-scale do the job. added 1 minute later PATT # 1 (make-scale 'c4 12 :alt '(1 5)) This is why I love Opusmodus ! Best !! Julio

Dear All, I have a little suggestion for workflow. 1) A simple context menu button (or some way) to open the XML snippet in other software. Like right-clicking on the snippet and have an option (OS based option) like "open with" (musescore, finale, sibelius, etc) This could be useful for collecting material for a piece to be edited outside Opusmodus. I personally use Musescore with my students. It's free, open and runs windows and mac. I also use Finale for myself. This simple options could solve the problem of the audition of many different snippets. 2) Another (much more complex) idea would be when click over each snippet to have a play panel, similar to the live coding panel (with play/stop button, tempo, volume, maybe sound and channel assigment , according to the number of staves, etc... This could be handy. Best, Julio added 2 minutes later Like this (when clicking over the snipett inside Opusmodus:

Some sieve values: PATT #53 (7 -1) PATT #59 (8 -1 -1) PATT #77 (13 -4 -2 -1) PATT #80 (-1 7) PATT #85 (-2 1 7) PATT #99 (-1 3 4) PATT #181 (1 3) PATT #186 (5 -1) PATT #295 (-1 6)

Yes ! Each pattern could be conceived as a sieve. PATT #1 could be like this: (setf patt '(1 5)) (setf pitches (gen-sieve '(c4 e6) patt :type :pitch)) Best, Julio