JulioHerrlein

In the jazz world, Barry Harris came up with the idea of harmonizing a bebop scale. Combining a C6 (C, E, G, A) and a Bdim7 (B, D, F, Ab) chords, we have this scale: From this stantpoint we can alternate tonic and dominant sounds, like this: Every pair of chords have all the 8-note set. The notes C,E, G and A are always harmonized with a C6 chord. The notes D, F, Ab and B are always harmonized with a Bdim7 chord. So, from the point of view of sets, there is no problem. WHAT IS NEEDED: I want a way to start FROM the melody, and then make a four part block harmonization with this (or any other) harmonic system from the melody as an OMN expression. So, I need a way to filter the notes to aply the right chord: FOR EXAMPLE: For the notes C, E, G and A If the note is an C (in any register), I will apply a chord like , I will add the notes A, G and E, below the melody. If the note is an (in any register), I will apply a chord like , I will add the notes G, E and C, below the melody. And so on... For the notes D, F, Ab and B: If the note is an B (in any register), I will apply a chord like , I will add the notes Ab, F and D, below the melody. And so on: So, to make any procedure: I need first find a way to apply a specific procedure only over the notes I want, over all the C notes, all the B notes, etc. How to filter from an OMN expression ? All the best ! Julio

Quoting André: But, despite this, we always want to have the output as close as possible to the final score. Best, Julio

WOWWWWWWW !!!! This version is getting better every day !!! Best ! Julio

Very interesting, André ! Two things: 1) How it works over chord lists, like '(c4e4g4) ? The chord is counted as one item in the span, or each note counts as one item ? 2) Would be interesting to have an argument for an "span-ignore-pauses" option, while doing the span, because the way you write the pause will chanbe the span function. Sometimes it can be good and sometimes not, depending on the desired effect. For example (-q -q) counts as 2 items, while (-h) counts as one item. Best, Julio

Thank you for your thougths and insights. Best Julio

Yes, this is exactly the way I see it. I was just thinking of chord symbols as another tool, because in my book I coded all the Forte numbers as chord symbols. As a jazz oriented musician chord symbols are very organic to me. I appreciate different viewpoints and and I think that music can originate from Any material, including popular music. In Brazil we have one of the most solid popular Expressions. All the best, Julio

Anyway, Opusmodus is amazing and can do A LOT for the composition process ! Best, Julio

Popular music is so important and fundamental. As jazz too... It could make Opusmodus more... popular ! Minimalistic music is related to it also. Best, Julio And chord symbols can be important in the compositional process, to track harmony changes. Actually, I use some advanced and crazy chord symbols that I invented to describe every kind of set (based on Forte list). Fr6 It's far more intuitive than 4-25, and it relates to the music history (french sixth chord...etc). Best, Julio Just my 2 cents...

Can the font and font size be changed in the text attributes function ? Best, Julio Maybe a "general-text" function could be added. A goodreason for that is to use in a more gramatical-based music, like the music made using functional harmony. Best

Would be Great to have a simple function to make chord symbols over staves...

Yes, Janusz ! I have this EXACT result when I evaluate the expression. The problem is when I do some chord processing, like chord-closest-path, like this: (setf comping (gen-repeat '(2) (gen-divide 1 (flatten (omn :pitch (chord-closest-path '(b3c4e4g4) '((h (b3 maj7) (d3 7)) (h (g3 maj7) (bb3 7)) (h (eb3 maj7) (eb3 maj7)) (h (a3 m7) (d3 7)) (h (g3 maj7) (bb3 7)) (h (eb3 maj7) (gb3 7)) (h (b3 maj7) (b3 maj7)) (h (f3 m7) (bb3 7)) (h (eb3 maj7) (eb3 maj7)) (h (a3 m7) (d3 7)) (h (g3 maj7) (g3 maj7)) (h (cs3 m7) (fs3 7)) (h (b3 maj7) (b3 maj7)) (h (f3 m7) (bb3 7)) (h (eb maj7) (eb maj7)) (h (cs3 m7) (fs3 7))))))))) and the resulting score comes without the symbols, like this: Is there some way of building my own chord library ? Best, Julio

When I did this post, I used the Giant Steps (Coltrane) progression as harmonic path, in this way: (setf harmpath '((h (b3 maj7) (d3 7)) (h (g3 maj7) (bb3 7)) (h (eb3 maj7) (eb3 maj7)) (h (a3 m7) (d3 7)) (h (g3 maj7) (bb3 7)) (h (eb3 maj7) (gb3 7)) (h (b3 maj7) (b3 maj7)) (h (f3 m7) (bb3 7)) (h (eb3 maj7) (eb3 maj7)) (h (a3 m7) (d3 7)) (h (g3 maj7) (g3 maj7)) (h (cs3 m7) (fs3 7)) (h (b3 maj7) (b3 maj7)) (h (f3 m7) (bb3 7)) (h (eb maj7) (eb maj7)) (h (cs3 m7) (fs3 7))) But in the resulting score, the chord symbols won't show. I have some questions: 1) How to make the chord symbols appear ? 2) How to make my own custom chord symbols ? 3) Can I make associations of chord symbols with specific sets of notes ? 4) Can I display chord symbols over a melody with a Hidden Piano Part playing them ? All the best ! Julio

Great!! Always good to see your loop functions!

Thank you, Stephane! You are always an inspiration! Best Julio

An important correction: In order to produce the right voicings is it necessary to sort the notes before transposing, so the Command to make the voicings over the original chord progression is like this: VOICINGS (setf chordprogdrop (chordize-list (pitch-transpose-n droplist (sort-desc (pitch-melodize chordtrp-rpt)))))

Thank you, Stephane! Best Julio

Thanks, Stephane !! Best ! Julio

Thank you !! Best ! Julio

Thank you, SB ! Sometimes we need to comunicate with machines, instead of musicians. Best, Julio

Thanks a lot, Stephane. I'm going to try your function soon. The idea here is more about transforming a set of chords, instead of generating the chords. More about controlling the exact spacing of the voicings in a given progression. I'm getting some trouble with gen-chord3. When evaluating this: (gen-chord3 '(c4 eb4 g4) '((3 3 3 3) (3 5 7 9) (2 5 7 11))) I'm getting different results each time First Time: Second time: Others: And so on... Is there some random algorithym in this function ? When evaluating this: (make-chord-if-length '((q c4 e d4 e4 f4 h d4)(s a4 b4 a4 g4 h f4)(q c4 d4 h e4))) I'm getting different results each time? Is this correct ? 1st time eval: 2nd time eval: 3rd eval... Best, Julio

Dear Wim, Please, check this post: Best, Julio

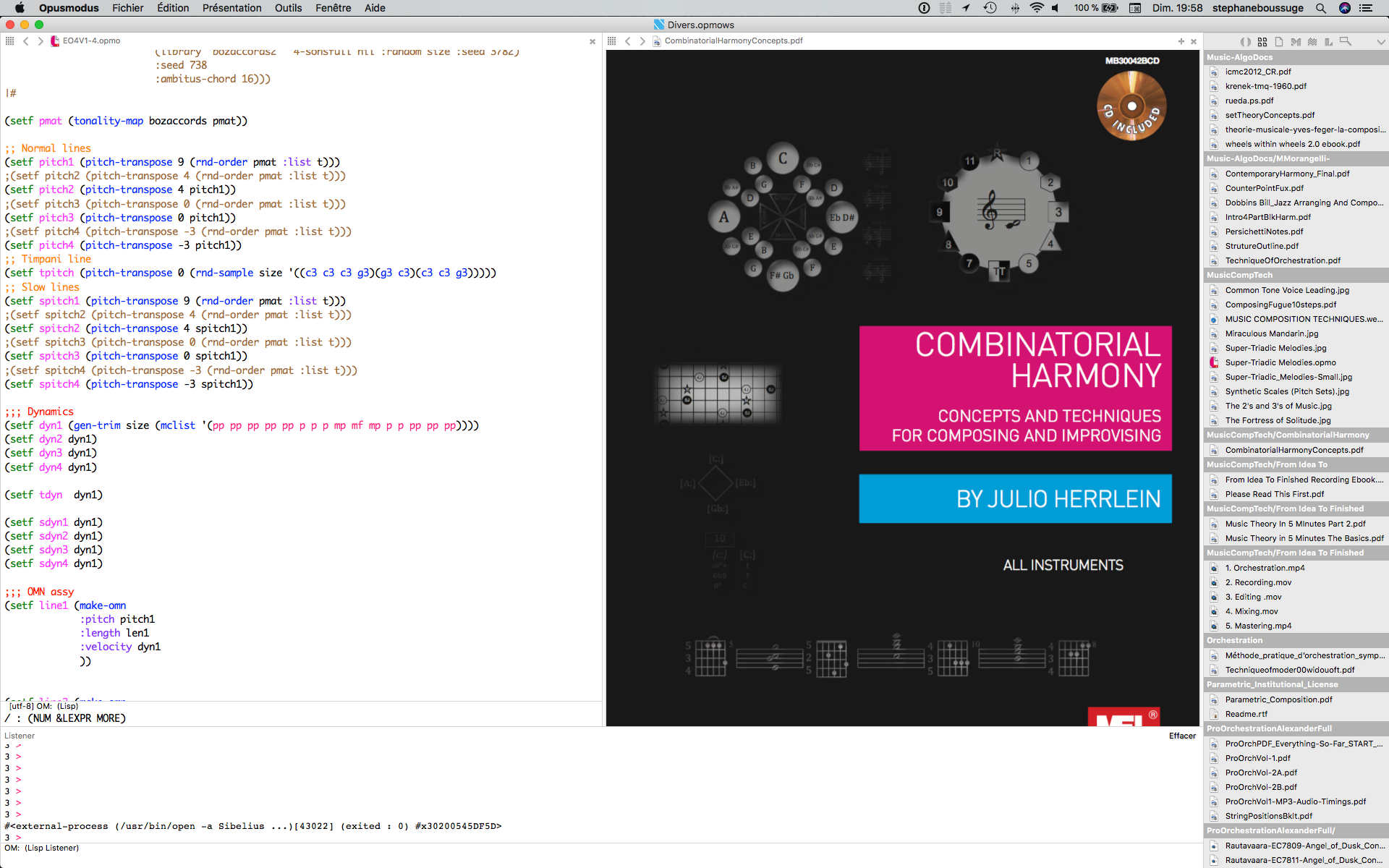
How to apply different voicings over a chord progression Sometimes you have to spread the notes of a chord progression in a very specific way, specially in the case of sectional writing as in the big bands, for example, where specific voicings are used, commonly named as drop2, drop3, etc. All the voicings are based in the initial closed position: - DROP2 is obtained by dropping the 2nd voice an octave below, as shown below: - DROP3 is obtained by dropping the 3rd voice an octave below, as shown below: There are 24 types of voicings as shown in the image below. The rule is to not exceed the octave between two adjacent voices. VOICING TYPES From Combinatorial Harmony Book, avaiable at: https://www.melbay.com/Products/Default.aspx?bookid=30042BCDEB CLOSED, DROP2, DROP3, DROP2+4, DROP2+3 and DOUBLEDROP2+ HOW TO IMPLEMENT IN OPUSMODUS EXAMPLE ;;; SOME Seventh CHORDS TO USE (setf chords '((a4c4d4f4) (c5eb4f4gs4) (d5f4g4bb4) (cs5e4fs4a4) (e4f4a4c4) (fs4g4b4d4) (d4eb4g4bb3) (eb4e4gs4b3) (e4g4a4c4) (a4c5d5f4) (f4gs4bb4cs4) (d4f4g4bb3) (fs5g4b4d5) (b5c5e5g5) (a5bb4d5f5) (gs4a3cs4e4) (b4d4e4g4) (d5f4g4bb4) (e5g4a4c5) (eb5fs4gs4b4) (e4f4a4c4) (fs4g4b4d4) (d4eb4g4bb3) (eb4e4gs4b3))) Setting the Voicing Types: csd (Closed Position) dp2 (Drop 2) dp2 (Drop 3) dp2-4 (Drop 2+4) dp2-3 (Drop 2+3) ddp2-3 (Double Drop 2 + Drop 3) (setf csd '(0 0 0 0) dp2 '(0 -12 0 0) dp3 '(0 0 -12 0) dp2-4 '(0 -12 0 -12) dp2-3 '(0 -12 -12 0) ddp2-3 '(0 -24 -12 0)) Drop order to apply over the sequence ;;;DROP ORDER (setf droplist (flatten (list csd dp2 csd dp2-4))) Command to make the voicings over the original chord progression ;;;ABERTURAS (chordize-list (pitch-transpose-n droplist (pitch-melodize chords))) RESULT Not the expected result!!!! See the next correction!!! All the best ! Julio Herrlein An important correction: In order to produce the right voicings is it necessary to sort the notes before transposing, so the Command to make the voicings over the original chord progression is like this: VOICINGS (setf chordprogdrop (chordize-list (pitch-transpose-n droplist (sort-desc (pitch-melodize chordtrp-rpt))))) Now, the right result for the voicing order csd dp2 csd dp2-4

Hello, Simple question: 1) How to specify in the articulation list for no displaying any articulation in the note without using "ord" ? 2) Is there some reset to "normal" articulation (without symbols) ? Best, Julio

Thanks, Lasse ! Glad you liked ! I'm also learning a lot. Best, Julio

Dear All, I'm trying to find a suitable workflow to make my choices easier. One idea was to compose over a piano reduction, for easier manipulation. Here's a way of doing that, with comments. The MIDI FILE output is like this. I did NO EDITIONS at all in Musescore.This is the video of the MIDI output. The XML output is the piano reduction. Very convenient ! Best, Julio str_4tet_opusmodus.mov ;;;SEV CHORDS Basic Functions ;;;Harmonic Functions/Sets List (setf Srm7 (pcs-transpose 9 (pcs '4-26) :pitch)) (setf S7M (pcs-transpose 4 (pcs '4-20) :pitch)) (setf Trm7 (pcs-transpose 4 (pcs '4-26) :pitch)) (setf T7M (pcs-transpose -1 (pcs '4-20) :pitch)) (setf Tam7 (pcs-transpose 11 (pcs '4-26) :pitch)) (setf D7 (pcs-transpose 11 (pcs '4-27b) :pitch)) (setf hd (pcs-transpose 9 (pcs '4-27) :pitch)) ;;;Estabilishing a Basic Progressions (setf chordprog (chordize (list Srm7 S7M Trm7 T7M Tam7 S7M))) ;;;Repeating and transposing the progression (setf chordtrp-rpt (pitch-transpose-repeat '((0 3 5 4) (0 2 -2 -1) (0 5 1 -2) (7 12 10 -3)) chordprog)) ;;; Making suitable voicings to the progression (setf chordprogdrop (chordize-list (pitch-transpose-n '(0 -12 0 0) (pitch-melodize chordtrp-rpt)))) ;;;Using these dropped chords as the source (setf chordprgtrp chordprogdrop) ;;;Opcionally with more Voice-Leading, with a smooth transition between the chords ;(setf chordprgtrp (chord-closest-path (car chordprogdrop) (gen-divide 4 chordprogdrop))) ;;;Counting the number of chords to make rhythm repetitions ;(setf times (get-count (get-count chordprgtrp))) ;;;Optionally setting manually the repetitions (setf times 24) ;;;Eachnote assigned to a voice (setf voz1 (flatten (pitch-demix 1 chordprgtrp))) (setf voz2 (flatten (pitch-demix 2 chordprgtrp))) (setf voz3 (flatten (pitch-demix 3 chordprgtrp))) (setf voz4 (flatten (pitch-demix 4 chordprgtrp))) ;;;optionally processing the ambitus of the voices ;(setf vozamb1 (ambitus '(c4 c5) voz1) vozamb2 (ambitus '(f3 c5) voz2) vozamb3 (ambitus '(g3 g4) voz3) vozamb4 (ambitus '(c2 e3) voz4)) ;;; Or setting to instrument's ranges ;(setf vozamb1 (ambitus (ambitus-instrument 'flute) voz1)vozamb2 (ambitus (ambitus-instrument 'oboe) voz2) vozamb3 (ambitus (ambitus-instrument 'clarinet) voz3) vozamb4 (ambitus (ambitus-instrument 'bassoon) voz4)) ;;;or just using the resulting drops as given (setf vozamb1 voz1 vozamb2 voz2 vozamb3 voz3 vozamb4 voz4) ;;;RIT ;;;one rhythm to all (for checking the "chorale" writing) ;(setf r1 (gen-repeat times '(q)) r2 (gen-repeat times '(q)) r3 (gen-repeat times '(q)) r4 (gen-repeat times '(q))) ;;;Doing an homorhythmic section (all instruments play the same rhythms (setf homorhy (gen-repeat times '(q -q e q e h h -s s s s)) r1 homorhy r2 homorhy r3 homorhy r4 homorhy) ;;; Articulation for the homorhytm (setf arthomo '(ten stacc ord stacc ord ord leg leg ord)) ;;;OMN ASSEMBLAGE of the Lines (setf vozomn1 (make-omn :length r1 :pitch vozamb1 :articulation arthomo :velocity (rnd-order'(p)))) (setf vozomn2 (make-omn :length r2 :pitch vozamb2 :articulation arthomo :velocity (rnd-order'(p)))) (setf vozomn3 (make-omn :length r3 :pitch vozamb3 :articulation arthomo :velocity (rnd-order'(pp)))) (setf vozomn4 (make-omn :length r4 :pitch vozamb4 :articulation arthomo :velocity (rnd-order'(pp)))) ;;;--------------------------------------------------------- ;;; SCORE ;;;---------------------------------------------------------- (def-score voices (:title "Piano-Red-4-Voices" :subtitle "Estudos Polifônicos" :composer "Julio-Herrlein" :key-signature 'atonal :time-signature '(4 4) :tempo '("Meditativo" q 60) :layout (piano-solo-layout '(pno-rh1 pno-rh2) '(pno-lh pno-lh2))) (pno-rh1 :omn vozomn1 :channel 1 :sound 'gm :program 'Violin :volume 100) (pno-rh2 :omn vozomn2 :channel 2 :sound 'gm :program 'Violin :volume 70) (pno-lh :omn vozomn3 :channel 3 :sound 'gm :program 'Viola :volume 80) (pno-lh2 :omn vozomn4 :channel 4 :sound 'gm :program 'Cello :volume 80))