-
Posts
792 -
Joined
-
Last visited
Content Type
Forums
Events
Store
Video Gallery
Posts posted by AM
-
-
dear david
this could be helpful for you... some basic-syntax-tutorials
have fun!
andré
well explainend
- opmo and Stephane Boussuge
-
 2
2
-
(defun prob-mutation (alist blist &key (factor 1) (prob-list nil)) (loop for a in alist for b in blist for x in (if (null prob-list) (cumulative-sums (gen-repeat (length alist) (float (/ factor (length alist))))) prob-list) when (probp x) collect b else collect a)) ;;; with linear prob-incf (prob-mutation (gen-repeat 100 1) (gen-repeat 100 2)) => (1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 2 2 1 1 1 1 2 2 1 2 2 2 1 1 1 1 1 2 1 1 1 1 1 2 2 1 1 2 2 1 1 2 2 2 2 1 1 2 2 2 1 1 2 1 1 1 1 2 2 2 2 2 2 2 2 2 1 2 2 2 2 1 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2) ;;; with an external prob-list 0 to 1.0 to 0 (setf half-sine (filter-first 100 (gen-sine 200 1 1.0))) (prob-mutation (gen-repeat 100 1) (gen-repeat 100 2) :prob-list half-sine) => (1 1 1 1 1 1 1 1 1 2 2 1 1 2 2 1 2 1 2 1 1 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 1 1 1 2 2 2 2 2 2 2 1 1 2 1 2 1 2 1 1 2 1 1 2 1 1 1 2 1 1) ;;; with an external prob-list 0 to 0.3 to 0 (setf half-sine (filter-first 100 (gen-sine 200 1 0.3))) (prob-mutation (gen-repeat 100 1) (gen-repeat 100 2) :prob-list half-sine) => (1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 1 1 2 1 1 1 1 1 2 1 2 1 1 2 1 2 1 2 1 1 1 2 1 1 1 2 1 1 2 1 1 2 1 1 1 2 1 1 1 1 2 1 2 1 2 1 1 1 1 1 2 1 1 2 2 1 2 1 2 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1)- Stephane Boussuge and erka
-
 1
1
-
 1
1
-
very nice, like a SIEVE!!
if it would be like:
(rnd-rest '(8 7 6 5 4 3 2 1) omn-seq)
you could manage the event-density in time...
or...
(rnd-rest '(0.1 0.2 0.23 0.4 0.7 0.6 0.3 0.43 0.91) omn-seq)
...perhaps also with (gen-envelope-tendency) (or something like that
just a spontanious idea

- opmo and Stephane Boussuge
-
 2
2
-
just a snippet... how i/you can use OPMO for some other things (TIME LAPS test mode, just to see if my code is working correctly).
i like the openness of the system.
- opmo and Stephane Boussuge
-
 2
2
-
-
 Practical Common Lisp
GIGAMONKEYS.COM
Practical Common Lisp
GIGAMONKEYS.COM- Stephane Boussuge and opmo
-
 2
2
-
funny
 but of course it is far far away from bach or a choral harmonization
but of course it is far far away from bach or a choral harmonization
I think there are various difficulties, on the one hand whether chatGPT finds enough information on the net about the harmonization of chorales and probably far too little about OPUSMODUS and LISP.
chatGPT doesn't really manage to program usefully in LISP (e.g. I tested sorting algorithms), but chatGPT explained to me extensively how the resulting code works, but it was always full of errorr/bugs. never worked, not fixable either. there is simply still a large amount of data missing for the system.
But of course I'm not a specialist, I just tried it (chatGPT) out in an amateurish way
-
-
was it not like...?
(rnd-sample-seq 2 '(1 2 3 4 5))
=> (1 2)
=> (3 4)
(rnd-sample-seq 3 '(1 2 3 4 5))
=> (2 3 4)
=> (3 4 5) -
what is the new name of the function "rnd-sample-seq"
thanx for a quick help!
andré -
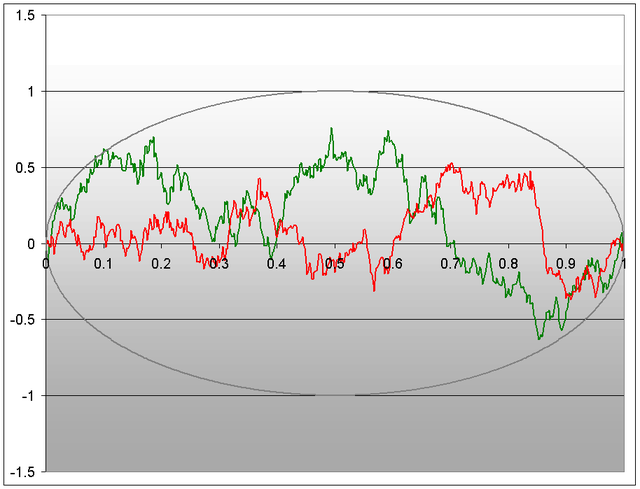
i like the concept of "brownian bridge" to produce complex curves from a to b, but not completely randomized or controlled. in the video you see all the generations for one evaluation...
how it could sound - mapped on different tonalities
Brownsche Brücke – Wikipedia
DE.WIKIPEDIA.ORGfor understanding in OPMO:
axiom: start end
(50 23)
gen1 => 1 step
(50 8 23)
gen2 => 3 steps
(50 15 8 -3 23)
gen3 => 7 steps
(50 40 15 13 8 -14 -3 29 23)
gen4 => 15 steps
(50 58 40 33 15 22 13 4 8 4 -14 -16 -3 17 29 17 23)
...and so on
-------------------------------------------------------------------------------
some evaluations with same AXIOM:
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;; BROWNIAN BRIDGE -> could be use as a rnd-process from A to B (integers or pitches) ;;; if you have a look to example with ":all-gen t", you will see the process with all generations, how it works ;;; or take a look to: ;;; https://de.wikipedia.org/wiki/Wiener-Prozess#/media/File:BrownscheBewegung.png ;;; https://de.wikipedia.org/wiki/Brownsche_Brücke ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;; SUB (defun pick (a b &key (span 5)) (let ((rnd1 (car (rnd-number 1 (+ a span) (- a span)))) (rnd2 (car (rnd-number 1 (+ b span) (- b span)))) (n)) (progn (setf n (car (rnd-number 1 rnd1 rnd2))) (if (or (= n a) (= n b)) (+ (rnd-pick '(1 -1)) n) n)))) (pick 2 3) ;;; MAIN ;;; MAIN (defun gen-brownian-bridge (n startend &key (all-gen nil) (output 'integer) (span 5)) (let ((seq)) (progn (setf seq (append (list startend) (loop repeat n with liste = startend do (setf liste (filter-repeat 1 (loop repeat (1- (length liste)) for cnt = 0 then (incf cnt) append (append (list (nth cnt liste) (pick (nth cnt liste) (nth (1+ cnt) liste) :span span) (nth (1+ cnt) liste)))))) collect liste))) (setf seq (if (equal all-gen t) seq (car (last seq)))) (if (equal output 'pitch) (integer-to-pitch seq) seq)))) ;;; EXAMPLES ;; SPAN influence -> span 2 (loop repeat 20 do (list-plot (gen-brownian-bridge 5 '(1.2 5.4) :span 2 :all-gen t) :zero-based t :point-radius 3 :join-points t) do (sleep 2)) ;; SPAN influence -> span 10 (list-plot (gen-brownian-bridge 5 '(50 23) :span 20 :all-gen t) :zero-based t :point-radius 3 :join-points t) ;;; SPAN default (5) (list-plot (gen-brownian-bridge 5 '(50 23) :all-gen t) :zero-based t :point-radius 3 :join-points t) (list-plot (gen-brownian-bridge 5 '(50 23)) :zero-based t :point-radius 3 :join-points t) (gen-brownian-bridge 5 '(50 23) :all-gen t :output 'pitch) (gen-brownian-bridge 5 '(50 23) :output 'pitch)- opmo, erka and Stephane Boussuge
-
 3
3
-
-
;;; quick-function (defun make-seq (&key (prob 0.5) (possible-pitches (make-scale 'c4 11))) ;; prob = length/rest-weight (make-omn :pitch (rnd-sample 10 possible-pitches) :length (gen-length (loop for i in (rnd-sum-to-size 20 10 '(1 2 3 4 5)) collect (if (probp prob) (* -1 i) i)) '1/16) :span :length)) ;;; EVAL (make-seq) (make-seq :possible-pitches (midi-to-pitch (gen-integer 10 110))) ;; with rnd-pitchesof course... with 60bpm
-
....or use some technology

Dirigierende Maschinen
WWW.TRANSCRIPT-VERLAG.DE
Eine musik- und technikgeschichtliche Abhandlung zur musikalischen Aufführungspraxis mit technischer Tempovermittlung. -
-
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; subfunction (defun reset-integer-sequence (alist &key (offset 0) (flatten nil)) (let ((min (find-min (flatten alist)))) (progn (setf alist (cond ((listp (car alist)) (loop for j in alist collect (loop for i in j collect (+ (- i min) offset)))) (t (loop for i in alist collect (+ (- i min) offset))))) (if (equal flatten t) (flatten alist) alist)))) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;; check it out ;; command-1 (list-plot (length-staccato (gen-length (reset-integer-sequence (ffth 6 0.075 (x-b (rnd-order '(44 52 22 23 13 44 68 6 22 9 73 28 68)) 3) :type 'integer)) 1/64) :value 1/64) :point-radius 2 :join-points t) (list-plot (length-staccato (gen-length (reset-integer-sequence (ffth 4 0.075 (x-b (rnd-order '(44 52 22 23 13 44 68 6 22 9 73 28 68)) 3) :type 'integer)) 1/64) :value 1/64) :point-radius 2 :join-points t)with 4 voices....
eval -> (command-3)
(defun reset-integer-sequence (alist &key (offset 0) (flatten nil)) (let ((min (find-min (flatten alist)))) (progn (setf alist (cond ((listp (car alist)) (loop for j in alist collect (loop for i in j collect (+ (- i min) offset)))) (t (loop for i in alist collect (+ (- i min) offset))))) (if (equal flatten t) (flatten alist) alist)))) ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; (setf s1 (make-omn :pitch '(c1) :length (length-staccato (gen-length (reset-integer-sequence (ffth 6 0.075 (x-b (rnd-order '(44 52 22 23 68 6 22 9 73 28 68)) 3) :type 'integer) :offset 4) 1/64) :value 1/32)) s2 (make-omn :pitch '(cs4) :length (length-staccato (gen-length (reset-integer-sequence (ffth 6 0.075 (x-b (rnd-order '(44 52 22 23 13 44 68 9 73 28 68)) 3) :type 'integer) :offset 4) 1/64) :value 1/32)) s3 (make-omn :pitch '(d5) :length (length-staccato (gen-length (reset-integer-sequence (ffth 6 0.075 (x-b (rnd-order '(44 52 22 23 68 6 22 9 73 28 68)) 3) :type 'integer) :offset 4) 1/64) :value 1/32)) s4 (make-omn :pitch '(ds7) :length (length-staccato (gen-length (reset-integer-sequence (ffth 6 0.075 (x-b (rnd-order '(44 52 22 23 68 6 22 9 73 28 68)) 3) :type 'integer) :offset 4) 1/64) :value 1/32))) (omn-to-time-signature (merge-voices s1 s2 s3 s4) '(4 4))- opmo and Stephane Boussuge
-
 2
2
-
@opmo: are there any plans for that?
-
- opmo and Stephane Boussuge
-
 2
2
-
oh, thx, did not know, that APPLY works on functions "first to the remaining arguments."!
-
if i understand you correctly....
you could COMPILE the score - and with :next-index t - you can keep all the versions
(compile-score 'myscore :file "My Score" :new-index t)"If :new-index is including as an argument the composer is able to collect as saved named incremented files compilation after compilation. This can be invaluable if the score has lots of randomised possibilities that need to be explored and compared to find the 'best version'."
-
some "ugly code" ...but it works....

you want to use (merge-voices) with ONE list as input?
(setf test '((w c2) (h c4 d4) (q g5 g5 g5 g5))) (defun your-merge-voices (alist) (merge-voices (first alist) (second alist) (third alist) (fourth alist) (fifth alist))) (your-merge-voices test) -
I would be very interested in it, since the interface over Midi is far too imprecise for reasonably complex rhythms, maybe an interface via Musicxml would be better?
-
if you adapt the code for LISPWORKS... could work like that
-
only trust your own code






position-insert-seq
in User Extensions Source Code
Posted
kind of ... "position-insert" with OVERWRITE
(defun position-insert-seq (&key alist insert item) (let ((pos (car (position-item item alist)))) (position-replace (gen-integer pos (+ pos (1- (length insert)))) insert alist))) (setf alist '(0 0 0 0 0 0 1 0 2 0 0 0 3 5 7)) (setf insert '(a b c d)) (position-insert-seq :alist '(0 0 0 0 0 0 1 0 2 0 0 0 3 5 7) :insert '(a b c d) :item 2) => (0 0 0 0 0 0 1 0 a b c d 3 5 7)